Here's another interesting PuzzlOR problem problem for the month of April:

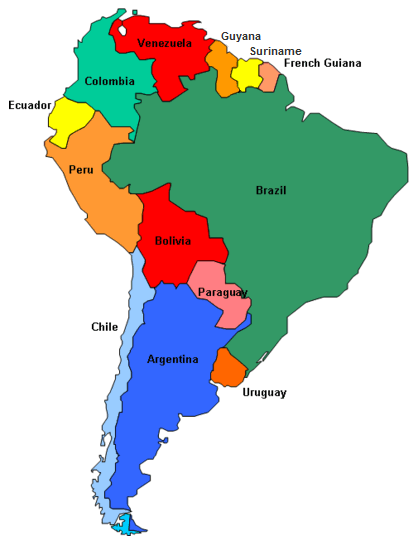
Your government has lost track of a high profile foreign spy and they have requested your help to track him down. As part of his attempts to evade capture, he has employed a simple strategy. Each day the spy moves from the country that he is currently in to a neighboring country.

The spy cannot skip over a country (for example, he cannot go from Chile to Ecuador in one day). The movement probabilities are equally distributed amongst the neighboring countries. For example, if the spy is currently in Ecuador, there is a 50% chance he will move to Colombia and a 50% chance he will move to Peru. The spy was last seen in Chile and will only move about countries that are in South America. He has been moving about the countries for several weeks.

Question: Which country is the spy most likely hiding in and how likely is it that he is there?

Let's import the necessary libraries and set up the model.

Now we will grab the names of the countries we'll be working with. We could could type it all in, but let's let pandas do the footwork by using the useful read_html method to scrape a relevant Wikipedia article:

We are given some huge clues on how to solve this problem. First of all, it has to do with transitions between discrete states in a finite state space. Second of all, the spy's strategy is based on random moves (it is a stochastic process). Third, the way that the spy's strategy is described we can tell that this stochastic process is memoryless.

Taken together, those three factors indicate that a Markov chain may be the best way to model the spy's movements. Let's begin by creating an adjacency matrix for these countries — that is, a matrix that indicates other countries to which the spy could move from any given country. By convention, this matrix is configured row-wise, so that the matrix element $a_{ij}$ represents whether it is possible for the spy to move to country $j$ (the column) from country $i$ (the row).

Now that we have figured out which countries are adjacent (that is, which other countries the spy could feasibly move to from each country), we can turn that into a stochastic matrix $A$ (also called the transition matrix) representing how likely each transition is conditioned on the spy being in a certain country.

In other words, we are normalizing the row vectors so that they represent probabilities, which is very easy in this problem because the spy is equally likely to move to any of the adjacent countries. That means we can normalize each row just by dividing it by its sum. To be concrete, we are taking each row of the adjacency matrix such as this one showing the countries we could move to from Argentina:

Using the knowledge that each adjacent country is an equally likely transition, we are turning this binary row of possibilities into a probability mass function of probabilities representing chance of being in each of the adjacent countries in the subsequent day:

After doing so, each row of our matrix constitutes a stochastic vector. Let's go ahead and carry out this transformation on the whole matrix:

Just as another concrete example, the fourth row of our new matrix ($i=3$ for our zero-based arrays) represents Chile. Conditioned on the spy being in Chile on day $t$, what are the probabilities that he will be in any given country on day $t+1$?

We are told that the spy started out in Chile on day $t=0$, so let's encode that in a linear algebra friendly way:

Like each row of the transition matrix, this column vector $x$ is a stochastic vector which represents probabilities. By setting the element corresponding to Chile equal to one, we are saying that we know the spy started there. However, if the problem were different, we could just as easily encode our beliefs about different probabilities with appropriate fractions.

To get from there to the probability on the next day, $t+1$, we can do the following:

$$x^\mathsf{T}A$$

How about on day $t+2$? We advance the probabilities by multiplying by $A$ again:

$$x^\mathsf{T} A A = x^\mathsf{T} A^2$$

We can easily generalize this by saying that our probability vector at any given day $t$ (having started in Chile on day $t=0$) is equal to $x^\mathsf{T} A^t$.

We are told that the spy has been moving around for "several weeks" — let's see what the probabilities are after 3 weeks:

We might worry that we are not being exact here in interpreting "several weeks" as exactly 21 days. What saves us is that this Markov chain converges to a steady state (called a stationary distribution) after a sufficient number of transitions.

For instance, here are the probabilities after different numbers of days:

It's pretty clear that, after a while, the probabilities converge to a steady state. Let's visualize this process. In the following graph, the $x$ axis will represent the number of transitions since the spy starts out in Chile on day $t=0$, and the $y$ axis will represent the probability of being in each country after that number of transitions.

What's more, we can see that after about a week it doesn't even matter where the spy originally started, as we can see by calculating $A^t$ where $t$ is greater than 10 or so:

No matter what the starting state was, the probabilities converge to the identical stationary distribution, with Brazil as the highest probability state at any given time. This should probably come as no surprise given that Brazil has the most adjacency with other nodes in this graph:

At this point, we can feel confident concluding that Brazil is the country most likely to contain the spy with $p(\mathrm{Brazil}) \approx 0.2$ after several weeks of moving around.

Thanks to John Toczek for producing the monthly PuzzlOR challenges.