I thought it would be interesting to do a post on what we can learn about a business with data analysis using solely open source intel — in other words, bringing together data sources which are publicly available but not necessarily meant to be analyzed by outsiders.
A few days ago, I was trolling around the Dunkin' Donuts store locator. By examining how store location data is requested and transmitted back to the user, I was able to scrape all of it together into one comprehensive table. The result was a data set with geographic and operational information on every single Dunkin' Donuts in the continental United States. In this post, we'll do some exploratory data analysis and visualization with this data set. We'll also examine some aspects of Dunkin's business by mashing the location data up with census and demographic data, and also data on franchisees munged from public filings.
The structure of the post will be to pose a series of hypothetical questions we might want to answer, and then trying to either answer it with the data we already have or go fishing for more open source data in order to figure it out.
Getting the data🔗
I noticed that each search result has some icons representing things like whether the store accepts loyalty cards, whether it sells K-cups, what co-branded company the store is located with (e.g. Hess gas station), and so on. Briefly wondering whether the data used to render these templates was easily available, I opened the Chrome developer tools to take a look at what was going on behind the scenes.

It turns out that Dunkin' Donuts is using MapQuest's enterprise platform to serve up data for their store locator in JSON format. Because all sorts of other data is stored and served in the same requests, the MapQuest API is presumably being used for other internal applications. While small chunks of data are transmitted to the browser of anybody who searches for store locations, we can actually assemble all of it just by making a few similar GET requests and tweaking the parameters for location, radius and max results.
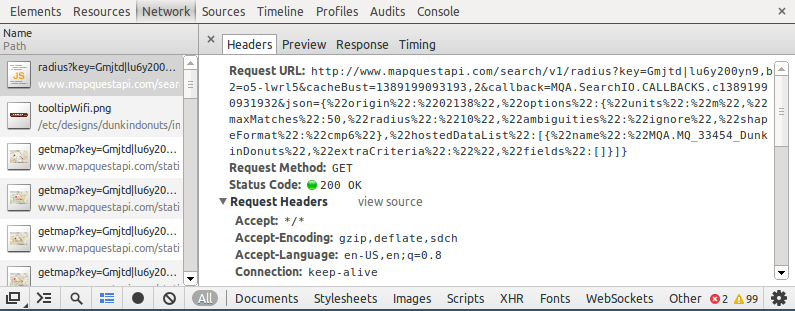
We'll save the data in a csv file for analysis. With that done, we can set up our analysis environment and dig in.
# import the tools we're going to work with
from __future__ import division
from mpl_toolkits.basemap import Basemap
import numpy as np
import pandas as pd
# set some options to make things look nicer
import seaborn as sns
sns.set_color_palette("Set1")
set1 = sns.color_palette("Set1")
set2 = sns.color_palette("Set2")
pd.set_option('display.max_columns', 20)
pd.set_option('display.max_rows', 20)
pd.set_option('show_dimensions', False)
# read in tables
fulldf = pd.read_csv('data/dd.csv')
hours = pd.read_csv('data/hours.csv')
# narrow the main df down to the columns we care about
wanted_cols = ['RecordId', 'Lat', 'Lng', 'address', 'city', 'state',
'postal', 'PhoneNumber', 'co_brander_cd']
df = fulldf[wanted_cols]
So here is what we have available:
df.head()
# store hours, can be joined with our main df on key `I`
hours.head()
# other fields that are in fulldf but we're not working with at the moment
print '\n'.join([c for c in fulldf.columns if c not in df.columns])
Where exactly are Dunkin' Donuts located?🔗
Living in Massachusetts, I am likely to be within sight of a Dunkin' Donuts at all times. But, the world is an unfair place, and not everyone is so fortunate.
Luckily, our data set came with specific lat/long coordinates, which makes it very easy to do some exploratory data analysis. We'll be using the Basemap toolkit for geographic visualizations. Because we'll be doing multiple visualizations with consistent styling, let's avoid repetition by creating a utility function to set up our maps for us:
def createmap(limits=[22, 50, -125, -67], figsize=(12, 12)):
""" create a Basemap object for plotting """
# get user defined latitude and longitude limits
llcrnrlat, urcrnrlat, llcrnrlon, urcrnrlon = limits
# create the Basemap object
fig, ax = plt.subplots(figsize=figsize)
m = Basemap(projection='merc',
llcrnrlat=llcrnrlat,
urcrnrlat=urcrnrlat,
llcrnrlon=llcrnrlon,
urcrnrlon=urcrnrlon,
resolution='l')
# set some aesthetic options
m.fillcontinents(color='white', lake_color='#eeeeee')
m.drawstates(color='lightgray')
m.drawcoastlines(color='lightgray')
m.drawcountries(color='lightgray')
m.drawmapboundary(fill_color='#eeeeee')
m.ax = ax
return m, fig, ax
With that done, let's just plot the whole data set and see what we're working with:
m, fig, ax = createmap()
x, y = m(np.array(df.Lng), np.array(df.Lat))
m.scatter(x, y, marker='o', c='#ff6200', s=8,
zorder=2, alpha=0.5, linewidth=0)
plt.show()
What are Dunkin' Donuts' administrative divisions and how many stores are in each?🔗
In the United States, franchising companies are required by the FTC to issue franchise disclosure documents (FDDs) to their potential franchisees. I was able to find Dunkin' Brands' 2011 filing here, from which we can gain some interesting insights into Dunkin's operations and business model.
For instance, here are their regional divisions:
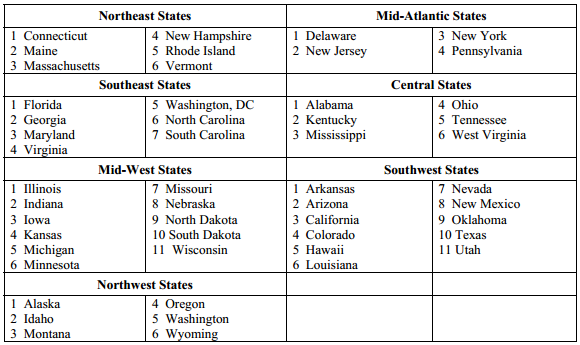
We can add these to the dataframe:
regions = pd.read_csv('data/regions.csv', usecols=range(1, 4))
regions.head()
Now that we have this data in a workable format, let's ask a question we can now answer that we couldn't before. Personally, I assumed that the Northeast states — a traditional Dunkin' stronghold — would easily have the most Dunkin' stores. That turns out not to be the case:
df.merge(regions[['state', 'region']]).groupby('region').RecordId\
.nunique().order(ascending=False)
Instead, the Mid-Atlantic states (DE, NJ, NY, PA) top the list.
What state has the highest number of Dunkin' locations per capita?🔗
Using US Census data (acquired here), we can easily answer that question.
# read the US gov't census data, keeping only the columns we care about
population = pd.read_csv('data/population.csv', usecols=(4, 5))
# get rid of the ugly, capital letter names that came in this csv
population.columns = ['state_name', 'pop2013']
# narrow down to states that actually contain store locations
mask = population.state_name.isin(regions.state_name)
population = population[mask]
# add the state abbreviations and reindex
population = population.merge(regions[['state', 'state_name']], on='state_name')
population = population.set_index('state')
# add locations by state and remove states with none
population['locations'] = df.groupby('state').RecordId.nunique()
population = population.dropna()
# figure out the quantity of interest and display the top 10
population['people_per_dunkin'] = population.pop2013 // population.locations
population.sort('people_per_dunkin').head(10)
That means that in my home state of MA, we take the prize with a staggering one Dunkin' Donuts for every 6,633 people! Let's take a much closer look at the population and demographics affecting how Dunkins are located within the most densely Dunkin'-ed state. To do this, I'll use a data set of population and demographic information on every MA zip code that I scraped from biggestuscities.com which itself repackages US census data.
What factors influence the placement of store locations?🔗
It seems intuitive that population will be the dominant factor in how many stores are situated in each zip code. But we could easily imagine that other demographic factors are also significant. For instance, we might wonder whether stores are more likely to be in wealthier or working class neighborhoods. Let's take a look:
# read in the MA demographics data
ma = pd.read_csv('data/ma.csv', usecols=range(5)).set_index('postal')
# count up dunkins per zip code
mask = df.state == 'MA'
ma_dunkins_by_zip = df[mask].groupby('postal').RecordId.count()
ma_dunkins_by_zip.name = 'dunkins'
ma = ma.join(ma_dunkins_by_zip)
# sort and display the top 5
ma.sort('dunkins', ascending=False).head()
One great tool for looking at multivariate relationships is a scatterplot matrix. Not only does it show what every variable's association looks like with respect to any other, looking along the diagonal shows each variable's marginal distribution.
from pandas.tools.plotting import scatter_matrix
axeslist = scatter_matrix(ma, alpha=0.8, figsize=(12, 12), c=set1[1], diagonal="kde")
for ax in axeslist.flatten():
ax.grid(False)
As expected, the dunkins variable's tightest and most obvious correlation involves population. The more people (or households), the more restaurant locations.
One obvious thing that this plot demonstrates very clearly is that population and the number of households are highly correlated. No surprise there, but it reminds us that in any model we might build, we would probably either want to (a) choose one of the two and avoid using the other, or (b) reduce the dimensionality with a method like PCA. The same goes for income per capita and median home value.
The term for this phenomenon is multicollinearity, and it's good practice to be careful about this before jumping into modeling. Let's look at the calculated correlations:
ma.corr()
Can we model the relationship between population and store locations?🔗
There doesn't necessarily look to be a strong linear correlation between number of Dunkins and any variable except population (or number of households). Simpler models are not always better, but although we might be able to squeeze some predictive power out of the other variables given a bit more legwork, it's often helpful to start with the most basic, "parsimonious" model (relevant Andrew Gelman post here).
Let's build a very simple regression model using pop2012 as the predictor variable for number of dunkins in a given zip code. We'll use a package called statsmodels, which will look very familiar to users of the R statistical package.
import statsmodels.formula.api as smf
# copy the dataframe so we can manipulate the `pop2012` column -- in
# order not to use such huge numbers (10k-60k) for population compared
# to much smaller numbers for dunkins (1-15), we'll divide population
# by 10,000 so it's roughly the same order of magnitude as the outcome variable
regression_df = ma[['pop2012', 'dunkins']].copy()
regression_df.pop2012 = regression_df.pop2012/10000.
# fit the model
results = smf.ols('dunkins ~ pop2012', data=regression_df).fit()
# print out results
results.summary()
So the equation is something like dunkins = 1.3 * (population/10,000) + 0.6.
Another way to do linear regression is using scikit-learn, the extremely popular machine learning library for Python. Of course, this will be somewhat overkill considering that we aren't even breaking the data up into train and test sets, but it may be useful to see this same modeling task carried out both ways.
from sklearn.linear_model import LinearRegression
# split the data into features and labels
X = ma.pop2012.values.reshape(-1, 1)/10000.
y = ma.dunkins.values
# fit the model
model = LinearRegression()
model.fit(X, y)
# print out the regression coefficients
coeffs = (model.coef_[0], model.intercept_)
print 'dunkins = %0.04f * (population/10,000) + %0.04f' % coeffs
# plot the results
fig, ax = plt.subplots(figsize=(10, 6))
# plot observed data with a small random y-axis jitter to avoid dots stacking up
jitter = np.random.rand(y.size)/2
plt.scatter(X, y + jitter, c=set1[1], label='observed')
# plot fitted prediction line
plt.plot(X, model.predict(X), c=set1[0], alpha=0.5, label='fit')
# set some aesthetic options
ax.set_xlim(0, X.max())
ax.set_ylim(0, y.max())
ax.set_xlabel('population (tens of thousands)')
ax.set_ylabel('dunkin locations')
plt.legend()
plt.show()
So what have we learned? Well, assuming that franchisees have opened up store locations based on some research and homework, and that stores which don't have enough demand eventually end up closing, it's probably reasonable to assume that this population model roughly represents the number of viable Dunkin' locations the market will bear at a given population level.
Is this usable? Well, let's say I am thinking about opening a DD franchise in Massachusetts. Naturally, I want to figure out the most profitable place to locate my brand new franchise. I certainly wouldn't want to plant myself somewhere that is already highly saturated unless I had some specific reason to believe I could catch some previously unmet demand. What I really want to know is this: which place might have enough population to support more Dunkin' locations than they currently have?
Let's take a look at the data:
# create a quick function to get the place name from the zip code
get_city_name = lambda x: df[df.postal == x].reset_index().ix[0, 'city']
# add the columns we're interested in
ma['predicted'] = model.predict(ma.pop2012.values.reshape(-1, 1)/10000.)
ma['gap'] = ma.predicted - ma.dunkins
ma['city'] = map(get_city_name, ma.index.values)
# show the top 10 potentially underserved zip codes
wanted_cols = ['pop2012', 'income_per_cap', 'dunkins', 'predicted', 'gap', 'city']
ma[wanted_cols].sort('gap', ascending=False).head(10)
Undoubtedly, many of these "Dunkin' gaps" are due to zoning and other stuff we could uncover once we start looking into specifics. However, now we have some candidate zip codes to start doing market research on instead of just guessing.
What co-brands does Dunkin' Donuts work with?🔗
One interesting feature in this data set is looking at other companies that Dunkin' Brands works with. You may have seen that Dunkin' Donuts are sometimes co-located with another business like a Stop & Shop grocery store (in the Northeast) or a Hess gass station.
By simple eyeballing of the dataframe grouped by co_brander_cd (and some judicious googling), I was able to put together a partial list of those co-brands:
cobrands = {
'ARA': 'Aramark',
'BCG': 'Boston Culinary Group',
'BRD': 'Baskin Robbins',
'BDT': 'Baskin Robbins',
'BP': 'BP',
'CIT': 'Citgo',
'CMB': 'Cumberland Farms',
'DEL': 'Delta',
'DNC': 'Delaware North Companies',
'EXX': 'Exxon',
'GLF': 'Gulf',
'HES': 'Hess',
'HMD': 'Home Depot',
'KUK': 'Lukoil',
'MOB': 'Mobil',
'OTG': 'OTG Management',
'PET': 'Petro',
'PM': 'Pathmark',
'SHL': 'Shell',
'SHW': 'Shaws',
'SOD': 'Sodexho',
'SR': 'Shop Rite',
'SS': 'Stop & Shop',
'SSP': 'SSP America',
'SUN': 'Sunoco',
'VAL': 'Valero',
'WH': 'WilcoHess',
'WLM': 'Walmart'
}
# add co-brands to our working dataframe
cobrands = pd.Series(cobrands, name='cobrand_name')
df = df.join(cobrands, on='co_brander_cd')
Let's see what other businesses have the most co-locations with Dunkin' Donuts:
cb = df.groupby('cobrand_name').cobrand_name\
.count().order(ascending=False).head(10)
cb
Any seasoned Dunkin' Donuts observer won't be surprised by the top 3 here — Hess and Dunkin' Brands have a longstanding strategic parternership, and the Baskin Robbins brand is actually also owned by Dunkin’ Brands Group, Inc.
Where are these co-brandings prevalent?🔗
# create the Basemap object
m, fig, ax = createmap(limits=[23, 47, -95, -65])
# get a list of the top 5 co-brands
top_5 = cb.head(5).index.values
# iterate through the top 5 and plot their locations
for i, name in enumerate(top_5):
mask = (df.cobrand_name == name)
lon, lat = np.array(df[mask].Lng), np.array(df[mask].Lat)
x, y = m(lon, lat)
m.scatter(x, y, marker='o', c=set1[i], s=15, zorder=i+3, linewidth=0,
label=name)
# plot all the rest
mask = ~(df.cobrand_name.isin(top_5))
lon, lat = np.array(df[mask].Lng), np.array(df[mask].Lat)
x, y = m(lon, lat)
m.scatter(x, y, marker='x', c='lightgray', label='other',
s=15, zorder=2, alpha=0.5, linewidth=1)
plt.legend(loc='lower right', fontsize=18)
plt.show()
What's the distribution of small or large franchisees?🔗
Also included in the Franchise Disclosure Document is a list of every single current franchisee. There are pages and pages of the pdf that look just like this:

Now we may be tempted to just throw this out as unusable information — it's in the dreaded pdf format after all — but at least all of these lines are in fairly standard, comma separated format. Using the command line utility pdftotext, I was able to dump text information from the desired pages to a text file.
wget -O DD_FDD_11.pdf http://www.bluemaumau.org/sites/default/files/DD_FDD%20UFOC%2003-26-10%20AMND%2011-23-10.pdf
pdftotext -f 126 -l 224 DD_FDD_11.pdf franchisees.txt
pdftotext -f 594 -l 626 DD_FDD_11.pdf franchisees2.txt
cat franchisees.txt franchisees2.txt > franchisees_all.txt
Using some (admittedly annoying and convoluted) regular expressions and little bit of manual cleanup, I was able to get this text into csv format and ready to import.
Note: looking at the address and phone number fields, you might worry (as I did) that this data could be considered personally identifiable information. Even though it is publicly available on the internet, we always want to avoid "doxing" private citizens for no reason. Don't worry though — this information pertains to the Dunkin' Donuts location, not the person.
franchisees = pd.read_csv('data/franchisees.csv')
franchisees
Keep in mind that this table is a couple years old (I found the 2011 version online and didn't feel like paying $99 for the 2013 FDD, and part of the fun of this hunt is using free, open source intel). Even so, it's pretty interesting.
franchisees.groupby('franchisee').franchisee\
.count().order(ascending=False).head(12)
Doing some quick googling, we find that the top two franchisees (Richard Lawlor and Stephen Williams) are executives for Hess and WilcoHess, respectively, two of Dunkin's biggest co-brands.
Now that we have this information, the next logical step is to connect it with our store location information. Luckily, Dunkin' Donuts has made this very easy for us by using the same foreign key RecordId in their FDD filing as in their MapQuest API!
# make a smaller df for joining with only the fields we care about
wanted_cols = ['RecordId', 'Lat', 'Lng', 'state']
franch_df = franchisees.merge(df[wanted_cols], on='RecordId')
franch_df
By default, merge operates a lot like SQL JOIN. In fact, it has a default keyword argument how='left' that reflects the SQL-like default LEFT INNER JOIN-style behavior, meaning that if records from the right-hand table don't match (in this case RecordIds in df that are different or missing), they will be dropped.
From the cell above, it looks like we only lost around 700 data points from missing or unmatched RecordId fields. We know that much of this is probably due to the store data in df being much more up to date than the franchisee data from 2011. Let's see if we can do a little better by trying to match some of the rest on phone numbers:
# pick the columns we want to use for joining
wanted_cols = ['PhoneNumber', 'Lat', 'Lng', 'state']
# figure out which rows we failed to match last time
not_matched = df[~df.RecordId.isin(franch_df.RecordId.values)]
# try to merge on phone number this time around
new_matches = franchisees.merge(not_matched[wanted_cols], on='PhoneNumber')
# add our newly matched stores to the working dataframe
franch_df = pd.concat((franch_df, new_matches))
Not bad — we were able to add over 100 records back in just by trying a different foreign key.
Where are these large franchisees' holdings geographically clustered in MA?🔗
Maybe we want see who the largest franchisees are in MA, one of DD's most heavily concentrated states:
m, fig, ax = createmap(limits=[41.4, 43.1, -73.6, -69.4], figsize=(13, 8))
# figure out the top 10 franchisees in MA
mask = (franch_df.state == 'MA')
ma_top = franch_df[mask].groupby('franchisee').franchisee\
.count().order(ascending=False)
# grab just the top 10 for plotting purposes
top_10 = ma_top.head(10).index.values
# get together a long-ish list of different colors to plot with
colors = set2[:6] + set1
# iterate through the top 10 and plot their locations
for i, name in enumerate(top_10):
mask = (franch_df.state == 'MA') & (franch_df.franchisee == name)
lon, lat = np.array(franch_df[mask].Lng), np.array(franch_df[mask].Lat)
x, y = m(lon, lat)
m.scatter(x, y, marker='o', c=colors[i],
s=15, zorder=i+3, linewidth=0,
label='%s (%d)' % (name, ma_top[name]))
# plot all the rest
mask = (franch_df.state == 'MA') & ~(franch_df.franchisee.isin(top_10))
lon, lat = np.array(franch_df[mask].Lng), np.array(franch_df[mask].Lat)
x, y = m(lon, lat)
m.scatter(x, y, marker='x', c='lightgray', label='other',
s=15, zorder=2, alpha=0.5, linewidth=1)
plt.legend(loc='upper right')
plt.show()
So here's an interesting insight: most of the largest franchisees in Massachusetts built their Dunkin' empires outside of the city, even though Boston proper has the highest concentration of store locations. While one of the top 10 (Mr. Goddess, as a director of Watermark Donut Co.) has most of his locations clustered in the Boston metro area, the others seem to focus their efforts mainly on more suburban or rural areas.
Why is this? I have basically no domain knowledge about Dunkin' Donuts or the hospitality industry, but I would surmise that it is much more capital intensive to invest in downtown real estate, and that there is quite a bit more competition in such a densely populated area.
What about the top franchisees for the whole country?🔗
Here are the top franchisees in the country. (We will leave out the two vice presidents of Hess and WilcoHess. Since they operate so many stores, the scatter plot would obscure other franchisees — see above in the plot of co-brands for their holdings.)
m, fig, ax = createmap(limits=[24, 47, -92, -65])
top_10 = franch_df.groupby('franchisee').franchisee\
.count().order(ascending=False).head(18).tail(16) # drop the top 2
# put together two color sets so we have enough for all the franchisees
colors = sns.color_palette('Set1', 8) + sns.color_palette('jet', 8)
# iterate through the top 10 and plot their locations
for i, name in enumerate(top_10.index.values):
mask = (franch_df.franchisee == name)
lon, lat = np.array(franch_df[mask].Lng), np.array(franch_df[mask].Lat)
x, y = m(lon, lat)
m.scatter(x, y, marker='o', c=colors[i],
s=15, zorder=i+3, linewidth=0,
label='%s (%d)' % (name, top_10[name]))
# plot all the rest
mask = ~franch_df.franchisee.isin(top_10)
lon, lat = np.array(franch_df[mask].Lng), np.array(franch_df[mask].Lat)
x, y = m(lon, lat)
m.scatter(x, y, marker='x', c='lightgray', label='other',
s=15, zorder=2, alpha=0.5, linewidth=1)
plt.legend(loc='lower right', fontsize=12)
plt.show()
One thing that is interesting here, and easily researched via Google, is that some franchisees, like Mr. Scrivanos, Mr. Andrade, Mr. Wolak, and Mr. Cafua are large independent holders whose business appears to center primarly around Dunkin' Donuts franchises, while some, like Mr. Colaianni and Mr. Weissberg, hold these franchises on behalf of large holding companies or banking/investment operations
Conclusion🔗
It's pretty amazing what kind of data is just freely available online for those willing to go digging, and how it can be mashed up in interesting combinations. Actually, this post is just scratching the surface — many states now keep all corporate filings in publicly searchable (and scrape-able!) databases online (e.g. MA Corporations Division). If we really wanted to start connecting all sorts of dots across different businesses, I think analyzing such data could be eye-opening. Some journalists are already starting to do this kind of thing in an attempt to dig up irregularities in political campaign donations.
Along these lines, there are some fascinating results emerging based on data sets just like this; for instance, check out this paper, titled "Geo-Spotting: Mining Online Location-based Services for Optimal Retail Store Placement." In it, the authors describe how Foursquare check-ins might be able to predict profitable places to put a coffee shop.
Actually, it even looks like Dunkin' Brands is hiring for people who can "Develop probabilistic models, use machine learning algorithms, Bayesian techniques to model business scenarios." Cool stuff.
FULL DISCLOSURE: I own one share of DNKN stock. Other than that, I have no affiliation with this company.